The Reasoning Revolution In AI: How We Got Here & Why It Matters
From Claude Shannon in the late 1940's to DeepSeek R1 and beyond.
This past January, when DeepSeek dropped its big reasoning model and everyone just went bonkers, I was heads-down building and didn’t have time to write anything about it. But I did do some work with the model, read the associated paper, and ended up doing an internal presentation for the Symbolic AI team on reasoning models.
We at Symbolic are building with these models in multiple senses of the term — we’re using these models in our AI coding tools, and we’re building user-facing products based on them — so I always try to keep our developers abreast of how new models work and how to think about them.
Today’s post is based on my internal reasoning model presentation, but expanded and in article form. It should be at a level that anyone familiar with some basic LLM concepts, like token windows and inference, can follow along and benefit from.
In the beginning was the token
I want to start this discussion by going back to Claude Shannon’s landmark 1948 paper, A Mathematical Theory of Communication. Even if you’re familiar with the concept of next token prediction that the paper introduced, bear with me, because I’m going to build on all of this to talk about how and why reasoning models work, and why they’re so important.
Shannon’s classic paper has pretty much all the core parts of the modern LLM revolution in it, both in terms of the basic mathematical concepts and also in how Shannon uses lookup tables and probabilities to manually produce what is almost GPT-2-class text output decades before the GPU was invented.
Shannon used randomness and probability tables to generate the sentences above by building on the observation that words in English tend to appear at different frequencies in text — conjunctions like “and” and “or” are more common than obscure nouns like “antidisestablishmentarianism,” for instance. Given a fragment of a sentence in English, you can plausibly complete the sentence by using a table of these probabilities to predict what words are likely to go at the end of the current fragment.
💡 Of course, everyone intuitively knows words occur at different frequencies, but here’s the crucial insight that makes Shannon’s invention of next token prediction work to build up word sequences that sound like real, intelligible, meaningful language: Out of all the words in the English dictionary, the word most likely to come next in a particular sentence fragment depends heavily on the previous words in the sentence.
So as you build a sentence word by word, the list of, say, the top five words most likely to come next changes as the sentence grows.
For example, consider the following two words: “Mary had”.
Native English speakers will all recognize that the most likely word (or “token” in AI speak) to come next in that sequence is “a”. And then, given “Mary had a”, we can all predict that “little” is most likely to come next.
But when we get to the word “little”, there’s a fork in the road at the deeper, more abstract level of meaning. In English, Mary could “have” (in the sense of ownership) a little (pet) lamb, or she could “have” (in the sense of eating, like having breakfast or lunch) a little (cooked) lamb. Which sense of the word “have” are we working with here?
It probably doesn’t truly matter which usage of “have” should govern the probabilities table for picking the very next word, because we’re still overwhelmingly likely to want to finish this off with the word “lamb.”
But note: the sentence fragment, “Mary had a little lamb”, can still support both senses of the term “have”.
If we want to keep adding tokens to this sequence, we need some way to decide which sense of the word “have” should govern the selection of future tokens.
✋ Alright, hold up: I’ve been dancing around a certain key concept by using the following vague phrases:
“sense of the word”
“sense of the term”
“usage”
“meaning”
We’re missing a term here — something with a meaning along the lines of, “a concept or cluster of concepts that this particular sequence of words seems to point to or to be related to somehow.”
I think that term is “region of latent space”, so let’s stop and explore it before we fully leave Claude Shannon and next token prediction behind.
Latent space
If you’re not familiar with the concept of latent space, here are a few previous articles of mine where the concept is introduced in different contexts:
In this post, I’d like to reintroduce it in a slightly more precise manner using the “Mary had a…” example I’ve been developing.
🧮 Technically speaking, latent space is a projection of shape in a higher-dimensional space to shape in a lower-dimensional space. Sort of like if you project a 3D cube onto a 2D plane, it makes a square.
Ok, what does that mean in English, though?
We must think of human language, both spoken and written, as extremely rich in data. To continue with our “Mary had a little lamb” example, we can greatly expand the number of possible meanings and nuances in that five-word phrase by adding a new token that means “emphasize this word.”
Consider the following variations on our phrase with emphasis added to a different word in each variation:
Mary had a little lamb. (But the other kids did not? Did they not have pets, or maybe they went hungry?)
Mary had a little lamb. (Presumably she doesn’t still have it, then? Or maybe she’s having something else now?)
Mary had a little lamb. (But not the little lamb… the one we’re talking about?)
Mary had a little lamb. (But not a big lamb? Or maybe not a lot of lamb?)
Mary had a little lamb. (As opposed to a little pony or some other animal? Or maybe as opposed to a little bit of some other type of food?)
So if we take our five words and our emphasis token (we should add the period as a stop token), then with just these seven tokens, there’s potentially a lot going on depending on the context.
Now imagine the corpus of 13 trillion tokens that GPT-4 was trained on, and you can start to grasp that if we were to plot each possible shade of meaning and degree of nuance in that corpus along its own axis, that would give us a space with an unmanageably high number of dimensions.
The idea of “latent space,” then, is that as the LLM is trained, it begins to group the inputs it’s seeing into higher-level abstractions that it can work with. If it sees many millions of sequences of words about pets, it begins to cluster those internally (via its weights) into something like a handful of related concepts that we humans would interpret as having to something to do with pets — pet food, domesticity, cats, dogs, houses, apartments, yards, collars, cages, and so on.
In other words, all of these many sentences about pets are collapsed or reduced or projected into a few points or regions of the model’s internal manifold of probabilities — which it uses to map inputs to outputs — that we might label as “the pet-ness regions of the model’s latent space” or just “the petness latents.”
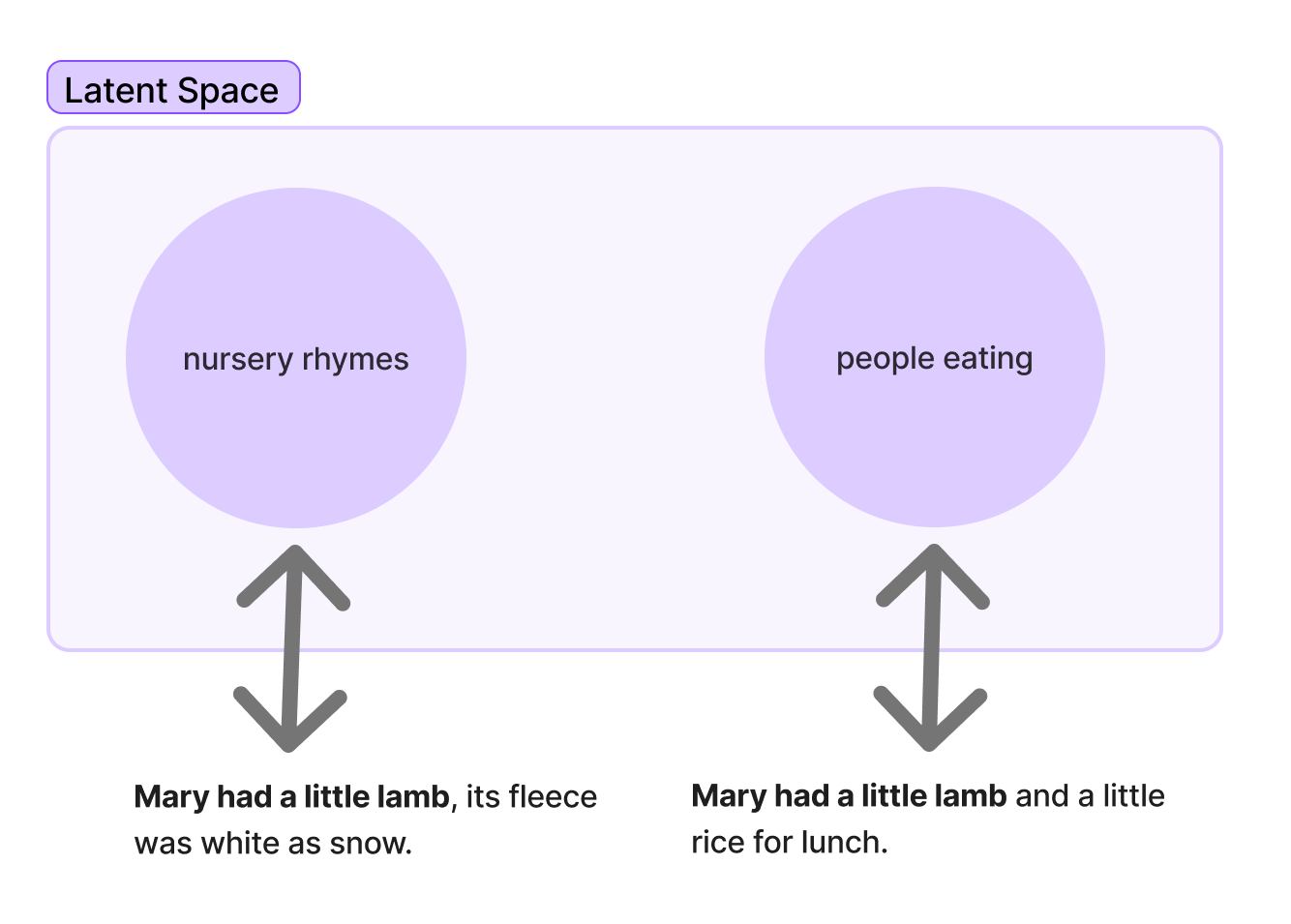
Now let’s go back to our “Mary had a little lamb” sentence:
You can see above that the differently completed sentences map to different regions of latent space. If the completion starts to go in the traditional direction of “its fleece…” then the rest of the tokens we’re going to find as we complete the sentence will be in the “nursery rhymes” region of latent space. Or, if we start in the direction of adding “and a little,” then we’ve navigated into the “eating” and maybe even “Mediterranean food” regions of latent space, and our next token predictions will reflect that.
Now that we have some basic concepts of next token prediction (based on conditional word probabilities) and latent space (i.e., reducing lots of information in the training data into a smaller number of more manageable, higher level concepts inside the model), let’s look at early attempts to do problem-solving with LLMs.
Early attempts at problem-solving with LLMs
It was hypothesized early on (and by early on I mean like 2020 — early in generative AI years, which are like fruit fly years) that if you could use next token prediction via a trained LLM to complete nursery rhymes, grocery lists, limericks, and other types of text artifacts, then perhaps you could use it to complete word problems.
Initial results in this area weren’t so great, though. A user would feed a basic word problem into an LLM as a prompt, then let the model’s next token predictions fire away and see if the resulting sequence of words amounted to the right answer.
Even if you weren’t paying attention to LLMs during this era, you can probably guess at the quality of the results researchers were getting with this approach. If the word problem you gave a model was a common one that was well-represented in its training data, then the odds were high that the model would produce the correct sequence of answer tokens. But if the word problem were novel, the model would reliably produce the wrong answer.
Then we discovered a trick called few-shot prompting. If you give the model some question and answer pairs, where the answer is correct, you might slightly increase the odds that you’ll get the correct answer at inference time.
Few-shot works pretty well for some types of completions, like if you’re asking the model to imitate a certain style of writing, or if you’re just trying to get it into the right conceptual ballpark. For instance, if we were to use few-shot as follows with our “Mary had a little lamb” example, we could reliably steer the model into either the “nursery rhyme” or “eating” regions of latent space:
But for solving word problems, this naive approach was still not great. The models were still getting the answer wrong most of the time. And to be honest, that’s exactly what we expected. There was no reason to believe an LLM trained on next token prediction should be able to solve a word problem. That seems nuts, right?
Then, in late 2022 and early 2023, researchers started to iterate their way into another trick, and things started to get weird.
Chain-of-thought prompting
The idea behind chain-of-thought (CoT) prompting is simple: When you’re providing the model with examples of the right way to do things, don’t just provide it with the “what” — also include as much detail about the “how” as you can. The model will then imitate both the answer part and the reasoning that leads up to the answer, thereby increasing the odds that its answer is correct.
By combining few-shot with CoT, we got a major step up in the accuracy of the model’s solutions to the problems we were putting to it.
You can see from the way I’ve color-coded the diagram above that with CoT, the model first generates its own reasoning about the problem (in imitation of the user-provided reasoning in the example), and then generates its answer. I’ve put the CoT tokens in a different color, denoting that we should consider them a different type of completion token, for a reason that hopefully will become clear later.
😵💫 If you’re wondering why this trick works so well, welcome to the club.
When few-shot CoT was discovered, it was not at all obvious that a model trained to predict the next word in a sentence should be able to “reason” well enough to solve a mathematical word problem (or any type of problem really), even if you jump-started its sequence building machinery with a sequence of tokens that amounted to detailed examples of such problem-solving.
To be clear: the answers to the problems we’re asking the LLM to solve are not anywhere in either the training data or the provided (few-shot) examples — there aren’t even any clues in the examples. All we’re giving it is a sequence of tokens that a human would interpret as “examples of how to go about solving a problem like this.” And yet it worked!
This was weird.
Why is it that if you give the model some examples of reasoning to imitate, it can imitate the reasoning itself sufficiently well to actually solve a word problem? (I have thoughts on an answer to this question, but more on that nearer the end of this post.)
Then we discovered yet another trick, and things got even weirder.
Zero-shot reasoning
The CoT approach that was pioneered in 2022 had two significant limitations:
Good examples of chain-of-thought that you can successfully prompt with are hard to generate. Some human has to come up with these high-quality CoT input tokens, and that takes time and effort.
Completion tokens are more expensive than input tokens, so by asking the model to generate a bunch of CoT completion tokens that you don’t care about and are going to throw away, you’re wasting money and electricity.
What the above boils down to is that CoT input tokens are expensive because humans have to work harder to come up with them, and CoT output tokens are expensive because they represent extra work for the LLM to do. It’s more work all around, and that’s not ideal.
But what if we could take at least one of those types of work out of the equation — specifically, the human labor of coming up with high-quality input tokens?
We know that the models can produce accurate CoT tokens if prompted properly, so maybe there’s some other way to prompt an LLM to do reasoning successfully that doesn’t involve giving them few-shot examples of CoT. After all, what are they really getting from the CoT input examples? Certainly, the provided examples don’t contain enough information to solve the target problem, so what if we could do away with them?
It turns out there is another prompting trick that works really well: all you have to do is ask the model to think step by step.
In the late 2022 paper, Large Language Models are Zero-Shot Reasoners, researchers figured out that you could get the model to generate CoT reasoning tokens without providing an example of the reasoning by simply asking it to think step by step.
In the paper, the researchers then use a second inference pass to get only the numerical answer from the text answer, but this is just a bit of clean-up — the model has (miraculously) already solved the problem in one inference pass with no CoT input tokens.
🌟 This bonkers result made a very bizarre and unexpected fact perfectly clear: LLMs trained on next token prediction can do reasoning and solve problems if you ask them in the right way, and it’s not a parlor trick, and they’re not just reproducing their inputs or training data.
When these results came out, the next step in the journey to AGI was clear: figure out a way to train models so that they’re even better at producing high-quality, accurate reasoning tokens that contain solutions to problems.
So while most of us were still marveling at the fact that LLMs could produce rap battles and chat dialogues, the race had quietly begun to train them LLMs produce long strings of verbal reasoning and thinking-out-loud problem-solving.
Boosting reasoning with reinforcement learning
If we want to train models to produce better reasoning token sequences using next token completion, the obvious way to do that is to show them many millions of examples of such reasoning during a pre-training run. But as I pointed out in my previous mention of the downsides to CoT prompting, high-quality reasoning examples are hard to come by in the wild.
It’s hard to search up a few relevant examples of CoT reasoning for a specific problem-solving inference pass, so there’s no way we can find enough examples of word problem => correct CoT => right answer in the wild.
But there is another way to train models than the traditional “Mad Libs” approach, where you show the LLM a sentence with a word missing and ask it to guess (or “predict”) the missing word/token. We can use a slower, more expensive, but very effective technique called reinforcement learning.
It’s this combination of reinforcement learning and the trick of targeting the quality of the reasoning tokens in training that might get us to AGI.
⏩ Read on for the details of how we might be able to scale our way to superintelligence with test-time computing, and stick around for a few thoughts on the implications for the US vs. China AGI arms race.
Here’s what’s behind the paywall:
Reinforcement learning basics
Using RL to improve reasoning
Scaling to superintelligence
Postscript: What does this mean for the AI arms race?
Reinforcement learning basics
I’ve written quite a bit on reinforcement learning, and indeed I still owe everyone another installment in that series. But if you’re not familiar with the concept, here’s a brief refresher, courtesy of a previous explainer of mine:
Reinforcement learning, then, is a technique with the following properties:
The model’s goal in an RL training scenario is to transform its environment from one state into some future hypothetical goal state by acting on it.
RL puts the model in a kind of dialogue with its environment through an observation => action => consequence loop that gets repeated over and over again. So the model makes an observation, then decides on and executes some action, and finally, it experiences a consequence while it also observes the new, altered state of its environment.
RL exposes the model to positive and negative consequences for selecting different actions, and the model takes these consequences along with a new observation of the latest state of the world as input into its next cycle. The RL literature calls this environmental feedback a “reward,” but to me, it’s weird to talk about a “negative reward,” which is possible in RL, so in this article, I often use the more neutral term “consequence.”
RL incorporates the concept of a long-term reward that the model is always trying to maximize as it makes the rounds of the observation => action => consequence loop. This way, the model isn’t strictly seeking only positive, immediate consequences on every turn of the loop, but can learn to take an action with a neutral or even negative consequence if that action will set it up for a larger payoff over the course of a few more turns.
Reinforcement learning is meant to mimic the way humans and animals actually learn things as they go through their lives and have experiences, and the results ML researchers have gotten from it are quite good. It’s especially strong in situations where supervised and unsupervised learning approaches are either weak or fail entirely, for instance when you don’t know what the correct output should be but you do know what’s incorrect.
So that’s the “RL” in a nutshell, and you can probably guess from the above that we need some sort of fast, preferably automated way of providing the model with the appropriate 👍 or 👎 signals during training. But before we talk about that, let’s look at how we can use RL to teach models to do better reasoning.
Using RL to improve reasoning
An ideal RL workflow for teaching a model to reason might have the following steps:
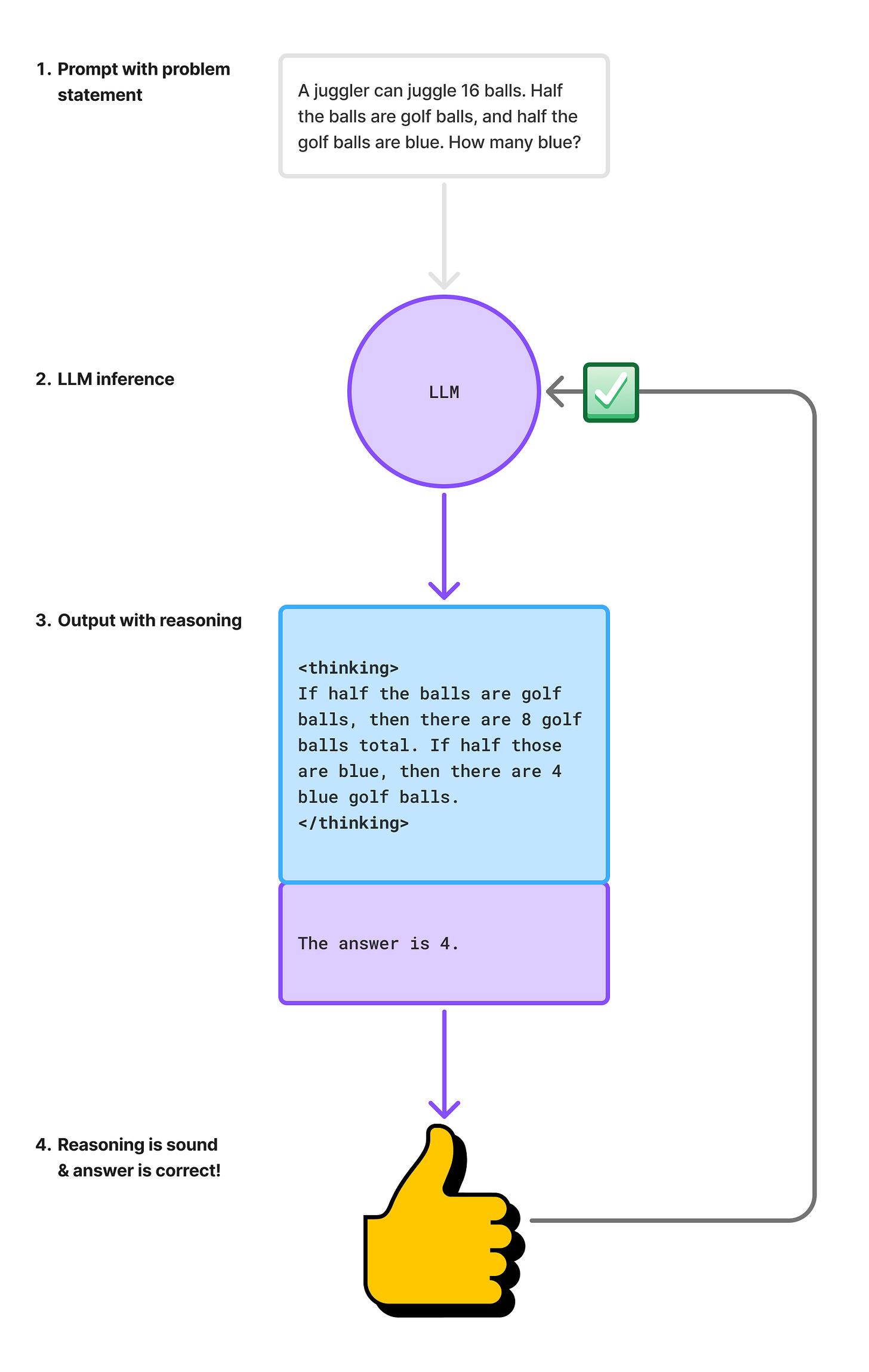
Let’s unpack this diagram:
We start with a prompt containing a word problem.
Next, we pass this prompt into the LLM, and the LLM produces a string of tokens — the first tokens it produces are reasoning tokens, and the final tokens are the answer that it reasoned its way to.
We then examine the answer and the reasoning, and confirm that the reasoning is sound and the answer is correct.
Because the model did what we wanted, we sent it a positive reward signal for adjusting its weights appropriately during the RL training session.
Note that in this process, we’re targeting the blue region of the token window. And when we do that, we’re also targeting something a bit deeper than just “these words are plausible and seem to match the distribution of words in some training exemplar.” Specifically, we’re trying to get the model to hone in on something more abstract, i.e., do the concepts in the chain of thought flow appropriately in order, and do they lead in a sensible and correct way to the right answer?
What I personally think is going on here is that we are looking not for a specific sequence of tokens but for a specific sequence of latents. What we’re really asking the model to do here, and what we’re evaluating its success at, is something like next latent prediction. This is what I think reasoning is — it’s next latent prediction.
Before we go deeper into this idea of next latent prediction, let’s back up and finish our story of how a reasoning model like DeepSeek R1 is actually trained, and why its training method caused many AI insiders to suddenly gain new confidence that we now have a path to artificial general intelligence (AGI) and even artificially super intelligence (ASI).
The trick is in how we evaluate the quality of the model’s reasoning output on each RL pass. Ideally, we’d want a human to read the output and check the work, but this would be super slow and won’t scale. So the next best thing we can do is use an LLM for this.
That’s right: a second “policy” LLM takes as input the output of the reasoning model we’re training, a it evaluates the quality of the reasoning and the correctness of the answer. Also, the policy LLM can itself be a reasoning model that uses reasoning to think through the evaluation.
Another improvement we can make on the scheme above is to have our reasoning LLM output multiple different reasoning + answer combinations, so that our policy model can pick the best one and send a reward signal based on that one. This is similar to how we use AI image generators like Midjourney, where you’re shown four different outputs and you, the user, pick the one you like best and maybe iterate on it further.
Scaling to superintelligence
Let’s look at a diagram of what our improved, LLM-based RL training process would look like:
You may have noticed something important: I put IQ scores on the models in my diagram.
Let’s say the RL model we’re training will, in the end, have an 112 IQ. (I know, IQ is controversial and it means nothing or it means everything or whatever… just go with it for the sake of explanation). The policy model we’re using to evaluate the reasoning output was trained on a previous version of this process, and it’s a little dumber at IQ 110.
So we use the dumber model to evaluate the reasoning of the model that we’re trying to make just a little bit smarter, and perhaps we know we’ve succeeded when the model we’re training is crushing it so hard that the dumber model can never find any flaws in its answers.
🚀 Now, the twist: After we’re done with this training run and we have a model that can reason reliably at IQ 112, what’s the next obvious move?
We turn the newly trained, smarter model into a policy model and set it to the task of evaluating the outputs of a new model that we want to train up to 117 IQ. And then when we’re done with that one, we swap out again and keep going. And we keep going and going and going until we either run out of electricity or we have our own electronic Claude Shannon on tap — a model so smart that we can ask it to write a sequel to Shannon’s work and advance the AI state of the art.
Right now, as far as I know, most efforts are focused on scaling problem-solving types of reasoning, but this isn’t the only type of reasoning we could target with these techniques. For instance, we could ask the model to find novel connections between apparently different concepts and optimize for creativity and analogical reasoning. Or, we could ask the model to draw useful contrasts between apparently similar concepts. Or, we could separate reasoning out into inductive and deductive, and target different types in different training passes.
My point is that there are different kinds of intelligences other than problem-solving, and if we can find ways to improve those through test-time compute we’d get closer to AGI even faster.
Test-time scaling
What I’ve just described is often called “test-time compute scaling”, i.e., you scale a model’s intelligence by using another model to test its outputs, and based on the results of that test, you adjust the first model’s weights.
The upside to test-time scaling is that we may well get to human-level reasoning and beyond with it.
The downside to test-time scaling is that you have to run tons and tons of inferences in order to train the model. Instead of running a single model and doing backpropagation to adjust weights, you’re running a full inference in the main model you’re training, then running a second full inference in the policy model, then adjusting the weights.
Even worse, in the case of both inferences — the main model and the policy model — you’re generating a ton of reasoning tokens. So these are not small, quick inferences, but rather very expensive ones that take a lot of energy.
All of this is why the hubbub about how DeepSeek R1 showed you don’t need lots of GPUs to scale model capabilities was completely insane.
These takes were just irredeemably, disqualifyingly bonkers, and this stuff was everywhere for about a week. It also didn’t help that DeepSeek may have lied about the number of GPUs it used in its training run, in order to hide some avoidance of sanctions on Chinese use of high-end GPUs.
It would be obvious to anyone who read the DeepSeek paper and understood it that reality is the opposite of what’s implied above — DeepSeek R1’s launch proved that GPU horsepower is even more valuable than we had imagined. With the method described here, you can run tons and tons of GPU-intensive inferences and climb the ladder to AGI with nothing but electricity. The more GPUs and electricity you have on tap, the faster you can climb.
Postscript: What does this mean for the AI arms race?
It’s worth asking not just how far up the intelligence ladder we can scale with these techniques, but also about the height of the ladder itself. This question of intelligence ladder height also has implications for the economics of AI. I do have some thoughts on these issues.
I’m not saying the following is definitely true, only that it scans to me:
“Intelligence” (whatever that is) is not an endlessly climbing exponential, but a sigmoid curve (see below), and humans are much closer to the upper limit than we are to the lower limit.
Following 1, AI scaling will approach the upper limit soon, and no matter how much GPU and data we keep throwing at it, progress will slow for everyone, and the delta between state-of-the-art and trailing edge will shrink rapidly.
(Background: The transformer architecture is an optimization. We could get the same performance out of a simpler network at much higher parameter counts). There are other, transformer-like optimizations out there that are yet to be discovered & that will let teams approach the upper limit with/ far fewer GPU and data resources.
Even without new optimizations, test-time scaling means you can just throw electricity at the problem. Countries that are building tons of nuclear reactors will be able to keep scaling even on trailing-edge hardware just by running all the GPUs they have without regard for cost.
If I’m right, then all of the above points are bearish for any company or country whose business is “AI” and whose moat is access to GPU cycles and data. Yes, I’m talking about NVIDIA, but also about the US, which is trying to retain an edge in AI via GPU export controls.
So it’s not clear to me that our export controls will slow China down enough so that we get there first. And it’s not like China isn’t reaching its own milestones in chip fabrication. Once they have the chips and the power plants, then if AGI is possible, they’ll reach it.